
알고 있으면 도움이 될만한 자료들을 올려두었습니다.
글 수 29
하나의 선분 AB가 있을 때, 그 선분상에 한 점 P를 구하여 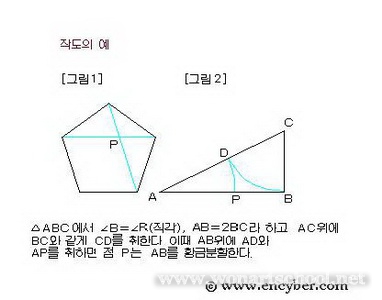
(AP)2=BP·AB
가 되도록 하는 일이다.
BP:AP=2:(√5 + 1)=1:1.61803…
을 황금비(黃金比) 또는 외중비(外中比)라 한다. 또, 정오각형의 같은 꼭지점[頂點]을 지나지 않는 두 개의 대각선(對角線)은 서로 다른 쪽 대각선을 황금분할한다. 황금비를 분수로 근사 표현을 하면 다음과 같다.

황금비는 고대 그리스에서 발견되었고, 가장 조화가 잡힌 비(比)로서 이와 같이 이름하게 된 것인데, 르네상스의 볼로냐의 수도승(修道僧) 루카 파치올리(Luca Pacioli)에 의하여 ‘신성비례(神聖比例)’라고 이름할 정도로 중요시되었다.
특히 시각(視覺)에 호소하는 도형이나 입체 등에서는 이 비를 많이 이용해왔으며, 예를 들면 직사각형의 두 변의 비가 황금분할이 되는 것은 여러 가지 비례의 직사각형 중에서 가장 정돈된 직사각형이라 하였다. 건축·조각·회화·공예(工藝) 등, 조형예술의 분야에서는 다양한 통일의 하나의 원리로서 널리 활용되고 있다.
또, 자연의 조화가 잡힌 형태 중, 예를 들면 잎맥[葉脈], 종자의 형상, 조개껍데기 소용돌이, 세포의 성장 등에서 이 비를 찾아내려고 하는 사람도 있다. 근년에는 음악 영역에서도 이것을 작곡에 활용한 예가 있다. 황금비는 일상 생활 속에서 쉽게 찾을 수 있다. 예를 들면 엽서, 담배갑이나 명함의 치수 등도 두 변의 비가 황금비에 가깝다. 물건을 선택할 때 대부분의 사람은 무의식 중에 황금비의 치수를 취하고 있다.







무의식중이라.....
^^* 앞으로 그림을 그릴 때 저것을 적용시켜봐야 겠네요~ㅎㅎㅎ